The Farquhar College of Arts and Sciences Division of Math, Science, and Technology will conclude the Mathematics Colloquium Series for fall 2010 with a pair of talks on Takagi’s Function. The presentations will take place on Wednesday, Dec. 1, from noon to 1:00 p.m., in the Mailman-Hollywood Building, room 311.
About the Presentations
—“Takagi’s Function: Construction and History,” presented by Bryan Candela, computer science major in the college
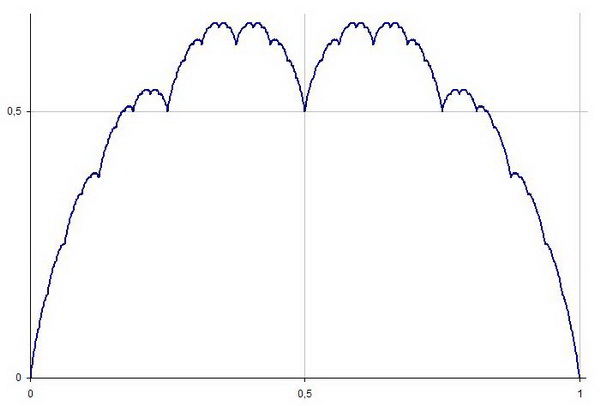
In this talk, Candela will explore the function, a continuous but nowhere differentiable curve. Constructed in 1903 by mathematician Teiji Takagi, this curve has many interesting properties. Candela will look at the construction of this map by the addition of “tent” maps, as well as discuss the history of Takagi, his function, and his work.
—“Takagi’s Function: Past and Present Results,” presented by Eric Samansky, Ph.D., assistant professor in the college
Even though Takagi’s Function is nowhere differentiable, one can ask whether it has an improper infinite derivative at any point. In this presentation, Samansky will present the answer to this question, which was recently proved by Pieter C. Allaart and Kiko Kawamura but has been worked on by several mathematicians over the past 80 years.
The Mathematics Colloquium Series, hosted by the Farquhar College of Arts and Sciences Division of Math, Science, and Technology, aims to increase awareness of mathematics’ importance and applications in daily life. The series also gives mathematics faculty members and students the opportunity to discuss independent research and share their passion for the subject.

